Co? Jak? Proč?

10 March 2017 — #art, #code, #java

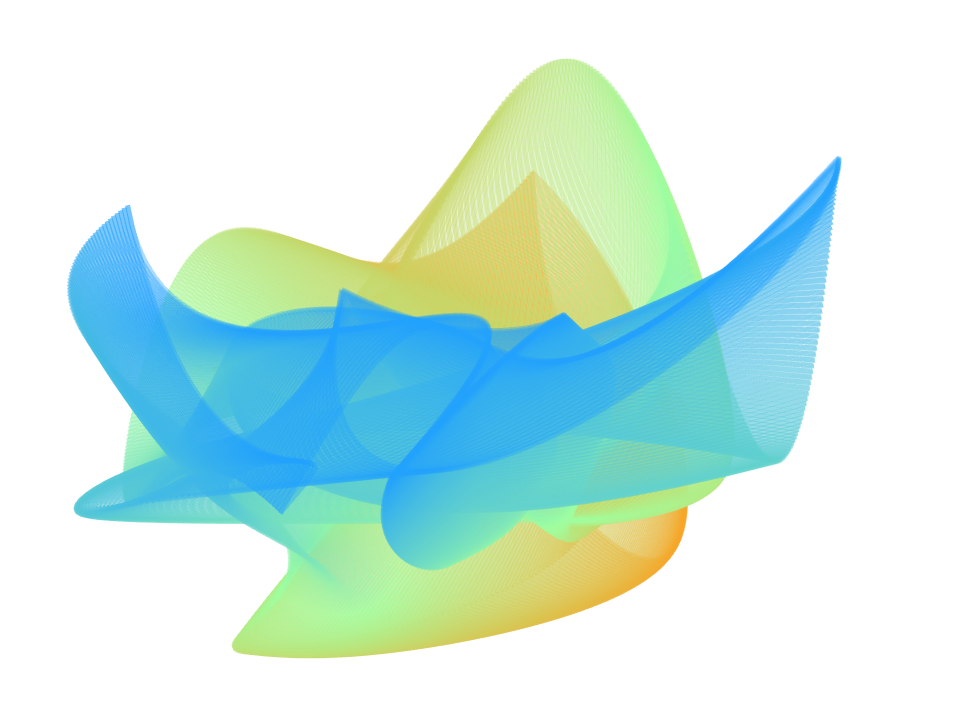
Bezier's curves in space and time

Ještě jako malý chlapec, když jsem sledoval hypnotické křivky spořiče obrazovky, to bylo v dobách, kdy tyto programy měly nějaký smysl. Na mysl se linuly základní otázky Co to je? Jak to funguje? Proč to …? A pak přišlo poznání. Ale nebylo to samo sebou. V dlouhém procesu učení jsou chyby právě tím, co vede ke správným odpovědím. Nořím se hlouběji do sítě a na každé nové úrovni znovu konvoluji.

Zdání dalšího rozměru prostoru je jenom výsledkem iluze perspektivy, stejně jako když Tom chytá Jerryho. Je to sice drobnost, ale když se nad ní zamyslíte, stejně jako nad Simpsonovími, možná vám dojde, že animované seriály nejsou vždy zase až tak hloupé. Ale k čertu s tím, to sem přeci vůbec nepatří. Jest-li je pes takový, jaký je jeho pán, pak stroj je notně obrazem svého programátora.

void setup()
{
  //fullScreen(P3D, 1);
  size(960, 720, P3D);
  bezierDetail(42);
  strokeWeight(5);
  frameRate(30);
  noFill();
  init();
}

int n = 5;         // pocet uzlu krivky
float m = 255;     // pocet krivek
float t = 0;       // pocatek casu
float dt = 0.02;   // casovy krok
float dl = -0.05;  // prostorove zpozdeni
float x0, y0;      // vychozi a konecny bod
float[][][] q = new float[n][6][4];
color red = color(255, 160, 32, 96);
color gre = color(160, 255, 160, 96);
color blu = color(32, 160, 255, 96);

void keyPressed() {saveFrame();}
void mouseClicked() {init();}

void draw()
{
  background(32);
  translate(width/2, height/2);
  
  for (int l = 0; l < m; l++) {
    x0 = o(t+l*dl, q[n-1][4][0], q[n-1][4][1], q[n-1][4][2], q[n-1][4][3]);
    y0 = o(t+l*dl, q[n-1][5][0], q[n-1][5][1], q[n-1][5][2], q[n-1][5][3]);
    beginShape();
    if (l < m/2) {
      stroke(lerpColor(red, gre, l/m*2));
    } else {
      stroke(lerpColor(gre, blu, (l-m/2)/m*2));
    }
    vertex(x0, y0);
    for (int i = 0; i < n; i++) {
      bezierVertex(
        o(t+l*dl, q[i][0][0], q[i][0][1], q[i][0][2], q[i][0][3]),
        o(t+l*dl, q[i][1][0], q[i][1][1], q[i][1][2], q[i][1][3]),
        o(t+l*dl, q[i][2][0], q[i][2][1], q[i][2][2], q[i][2][3]),
        o(t+l*dl, q[i][3][0], q[i][3][1], q[i][3][2], q[i][3][3]),
        o(t+l*dl, q[i][4][0], q[i][4][1], q[i][4][2], q[i][4][3]),
        o(t+l*dl, q[i][5][0], q[i][5][1], q[i][5][2], q[i][5][3])
      );
    }
    endShape();
  }
  
  t += dt;
}

float o(float t, float a, float b, float c, float d)
{ // souradnice bodu dane harmonickou funkci v case
  return a * sin(t/b) + c * cos(t/d);
}

float[] p(int lim)
{ // nahodne parametry pro vypocet souradnice
  float[] param = new float[4];
  param[0] = random(lim/2);
  param[1] = random(1, 11);
  param[2] = random(lim/2);
  param[3] = random(1, 11);
  return param;
}

void init()
{ // inicializace parametru krivek
  for (int i = 0; i < n; i++) {
    for (int j = 0; j < 6; j++) {
      if (j % 2 == 0) {
        q[i][j] = p(width);
      } else {
        q[i][j] = p(height);
      }
    }
  }
}

Na plochém dvourozměrném plátně tvořeném pravidelným uspořádáním pixelů a ve čtyřech dimenzích prostoru barev se nachází bod. Dva body na náhodných souřadnicích dávají dohromady přímku a pomocí dvou přímek již lze definovat Bézierovu křivku. Pak už jen stačí pár takových křivek spojit dohromady a můžete bez ohledu na vytyčené hranice začít čarovat…

Astro-Grázl

Zdrojový kód Všehomíra

Co? Jak? Proč?